MHKiT Wave Module
The following example runs an application of the MHKiT wave module to 1) read in NDBC data, 2) compute metrics from spectral data, 3) generate a capture length matrix, 4) calculate MAEP, and 5) plot the matrices.
Start by importing the necessary python packages and MHKiT module.
[1]:
import numpy as np
import pandas as pd
from mhkit import wave
Load NDBC Data
We can use MHKiT to load data downloaded from https://www.ndbc.noaa.gov.
[2]:
ndbc_data_file = "data/wave/data.txt"
# ndbc.read_file outputs the NDBC file data into two variables.
# raw_ndbc_data is a pandas DataFrame containing the file data.
# meta contains the meta data, if available.
[raw_ndbc_data, meta] = wave.io.ndbc.read_file(ndbc_data_file)
raw_ndbc_data.head()
c:\users\sterl\codes\mhkit-python\mhkit\wave\io\ndbc.py:99: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
data = pd.read_csv(
[2]:
| 0.0200 | 0.0325 | 0.0375 | 0.0425 | 0.0475 | 0.0525 | 0.0575 | 0.0625 | 0.0675 | 0.0725 | ... | 0.3300 | 0.3400 | 0.3500 | 0.3650 | 0.3850 | 0.4050 | 0.4250 | 0.4450 | 0.4650 | 0.4850 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018-01-01 00:40:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.03 | 0.04 | 0.09 | 0.22 | 0.22 | ... | 0.07 | 0.08 | 0.07 | 0.07 | 0.03 | 0.01 | 0.02 | 0.01 | 0.01 | 0.0 |
| 2018-01-01 01:40:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.02 | 0.06 | 0.08 | 0.21 | 0.21 | ... | 0.07 | 0.07 | 0.08 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 | 0.00 | 0.0 |
| 2018-01-01 02:40:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.08 | 0.07 | 0.14 | 0.32 | ... | 0.08 | 0.06 | 0.05 | 0.03 | 0.03 | 0.02 | 0.01 | 0.01 | 0.00 | 0.0 |
| 2018-01-01 03:40:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.13 | 0.22 | 0.26 | 0.32 | ... | 0.05 | 0.06 | 0.05 | 0.03 | 0.03 | 0.01 | 0.01 | 0.00 | 0.00 | 0.0 |
| 2018-01-01 04:40:00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.03 | 0.14 | 0.17 | 0.37 | 0.40 | ... | 0.06 | 0.12 | 0.04 | 0.04 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.0 |
5 rows × 47 columns
The resulting DataFrame is spectra indexed (rows) by datetime with frequency as the columns. To use this data in MHKiT functions we must first transpose the DataFrame
[3]:
# Transpose raw NDBC data
ndbc_data = raw_ndbc_data.T
ndbc_data.head()
[3]:
| 2018-01-01 00:40:00 | 2018-01-01 01:40:00 | 2018-01-01 02:40:00 | 2018-01-01 03:40:00 | 2018-01-01 04:40:00 | 2018-01-01 05:40:00 | 2018-01-01 06:40:00 | 2018-01-01 07:40:00 | 2018-01-01 08:40:00 | 2018-01-01 09:40:00 | ... | 2018-01-31 14:40:00 | 2018-01-31 15:40:00 | 2018-01-31 16:40:00 | 2018-01-31 17:40:00 | 2018-01-31 18:40:00 | 2018-01-31 19:40:00 | 2018-01-31 20:40:00 | 2018-01-31 21:40:00 | 2018-01-31 22:40:00 | 2018-01-31 23:40:00 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0200 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.00 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0325 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.00 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0375 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.00 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0425 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.00 | 0.0 | 0.0 | 0.0 | 0.00 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0475 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.01 | 0.0 | 0.0 | 0.0 | 0.0 | ... | 0.06 | 0.0 | 0.0 | 0.0 | 0.07 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
5 rows × 743 columns
Compute Wave Metrics
We will now use MHKiT to compute the significant wave height, energy period, and energy flux.
[4]:
# Compute the enegy periods from the NDBC spectra data
Te = wave.resource.energy_period(ndbc_data)
Te.head()
[4]:
variable
2018-01-01 00:40:00 7.458731
2018-01-01 01:40:00 7.682413
2018-01-01 02:40:00 7.498263
2018-01-01 03:40:00 7.676198
2018-01-01 04:40:00 7.669476
Name: Te, dtype: float64
[5]:
# Compute the significant wave height from the NDBC spectra data
Hm0 = wave.resource.significant_wave_height(ndbc_data)
Hm0.head()
[5]:
variable
2018-01-01 00:40:00 0.939574
2018-01-01 01:40:00 1.001399
2018-01-01 02:40:00 0.924770
2018-01-01 03:40:00 0.962497
2018-01-01 04:40:00 0.989949
Name: Hm0, dtype: float64
[6]:
# Set water depth to 60 m
h = 60
# Compute the energy flux from the NDBC spectra data and water depth
J = wave.resource.energy_flux(ndbc_data, h)
J.head()
[6]:
variable
2018-01-01 00:40:00 3354.825613
2018-01-01 01:40:00 3916.541523
2018-01-01 02:40:00 3278.298930
2018-01-01 03:40:00 3664.246679
2018-01-01 04:40:00 3867.014933
Name: J, dtype: float64
Note on data types
MHKiT functions typically allow Pandas Series, Pandas DataFrame, or xarray DataArray input. Multidimensional data (DataFrames and DataArrays) typically require an index or dimension name to specify the frequency or time dimension in question. If not supplied, the first dimension is assumed to be the relevant dimension.
The above results (energy period, energy flux, and significant wave height) were returned as Pandas Series. 2D wave spectral data (frequency x time) was input and the frequency dimension was reduced leaving 1D, columnar data as the output. In Pandas, this is represented as a Series. If a DataArray with 3 or more dimensions was input, the output would be a DataArray with one fewer dimensions.
Generate Random Power Data
For demonstration purposes, this example uses synthetic power data generated from statistical distributions. In a real application, the user would provide power values from a WEC. The data is stored in pandas Series, containing 743 points.
[7]:
# Set the random seed, to reproduce results
np.random.seed(1)
# Generate random power values
P = pd.Series(np.random.normal(200, 40, 743), index=J.index)
Capture Length Matrices
The following operations create capture length matrices, as specified by the IEC/TS 62600-100. But first, we need to calculate capture length and define bin centers. The mean capture length matrix is printed below. Keep in mind that this data has been artificially generated, so it may not be representative of what a real-world scatter diagram would look like.
[8]:
# Calculate capture length
L = wave.performance.capture_length(P, J)
# Generate bins for Hm0 and Te, input format (start, stop, step_size)
Hm0_bins = np.arange(0, Hm0.values.max() + 0.5, 0.5)
Te_bins = np.arange(0, Te.values.max() + 1, 1)
# Create capture length matrices using mean, standard deviation, count, min and max statistics
LM_mean = wave.performance.capture_length_matrix(Hm0, Te, L, "mean", Hm0_bins, Te_bins)
LM_std = wave.performance.capture_length_matrix(Hm0, Te, L, "std", Hm0_bins, Te_bins)
LM_count = wave.performance.capture_length_matrix(
Hm0, Te, L, "count", Hm0_bins, Te_bins
)
LM_min = wave.performance.capture_length_matrix(Hm0, Te, L, "min", Hm0_bins, Te_bins)
LM_max = wave.performance.capture_length_matrix(Hm0, Te, L, "max", Hm0_bins, Te_bins)
# Show mean capture length matrix
LM_mean
[8]:
| y_centers | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | 14.0 | 15.0 | 16.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x_centers | |||||||||||||||||
| 0.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 0.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.120286 | 0.053376 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1.0 | NaN | NaN | NaN | NaN | NaN | NaN | 0.110686 | 0.068070 | 0.049452 | 0.065912 | NaN | 0.056593 | 0.029950 | 0.017234 | NaN | NaN | NaN |
| 1.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.019749 | 0.018673 | NaN | NaN | 0.012473 | 0.011205 | 0.012307 | 0.010432 | NaN | NaN |
| 2.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.013882 | 0.012547 | 0.009672 | 0.008770 | 0.008585 | 0.007525 | 0.005272 | 0.007809 | NaN | NaN |
| 2.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.007244 | 0.006488 | 0.005788 | 0.005652 | 0.005180 | 0.004260 | 0.003623 | 0.004509 | NaN |
| 3.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.004500 | 0.005660 | 0.004691 | 0.004109 | 0.003952 | 0.003104 | 0.003408 | 0.002291 | 0.001792 | NaN |
| 3.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.003924 | 0.003674 | 0.003020 | 0.002746 | 0.002247 | 0.002000 | 0.002257 | 0.002033 | NaN |
| 4.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.003185 | 0.002513 | 0.002386 | 0.002147 | 0.002246 | 0.001605 | 0.001730 | NaN | NaN |
| 4.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.002343 | 0.002087 | 0.001919 | 0.001590 | 0.001438 | NaN | NaN | NaN | NaN |
| 5.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.001913 | 0.001720 | 0.001716 | 0.001411 | 0.001219 | 0.001345 | NaN | NaN | NaN |
| 5.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.002101 | 0.001516 | 0.001331 | 0.000902 | 0.001033 | NaN | NaN | NaN | NaN |
| 6.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.001097 | 0.000895 | NaN | 0.000858 | 0.000987 | NaN | NaN | NaN |
| 6.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000837 | 0.001024 | 0.000419 | NaN | 0.000688 | NaN | NaN | NaN |
| 7.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000461 | 0.000633 | NaN | NaN | NaN |
| 7.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000553 | NaN | NaN | 0.000312 | 0.000437 | NaN | NaN |
| 8.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000443 | 0.000351 | NaN |
| 8.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000418 | 0.000405 |
| 9.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 9.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000153 | NaN |
| 10.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000281 |
| 10.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 0.000204 | 0.000225 |
Additional capture length matrices can be computed, for example, the frequency matrix is computed below.
[9]:
# Create capture length matrices using frequency
LM_freq = wave.performance.capture_length_matrix(
Hm0, Te, L, "frequency", Hm0_bins, Te_bins
)
# Show capture length matrix using frequency
LM_freq
[9]:
| y_centers | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | 14.0 | 15.0 | 16.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x_centers | |||||||||||||||||
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.002692 | 0.001346 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 1.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.001346 | 0.006729 | 0.004038 | 0.001346 | 0.000000 | 0.002692 | 0.002692 | 0.001346 | 0.000000 | 0.000000 | 0.000000 |
| 1.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.005384 | 0.002692 | 0.000000 | 0.000000 | 0.009421 | 0.004038 | 0.006729 | 0.005384 | 0.000000 | 0.000000 |
| 2.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.002692 | 0.005384 | 0.018843 | 0.018843 | 0.029610 | 0.021534 | 0.001346 | 0.002692 | 0.000000 | 0.000000 |
| 2.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.013459 | 0.052490 | 0.055182 | 0.018843 | 0.025572 | 0.022880 | 0.005384 | 0.001346 | 0.000000 |
| 3.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.001346 | 0.021534 | 0.044415 | 0.047106 | 0.020188 | 0.012113 | 0.010767 | 0.010767 | 0.001346 | 0.000000 |
| 3.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.006729 | 0.040377 | 0.029610 | 0.047106 | 0.004038 | 0.008075 | 0.004038 | 0.001346 | 0.000000 |
| 4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.009421 | 0.017497 | 0.029610 | 0.040377 | 0.002692 | 0.004038 | 0.005384 | 0.000000 | 0.000000 |
| 4.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.016151 | 0.013459 | 0.017497 | 0.022880 | 0.012113 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 5.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.002692 | 0.008075 | 0.008075 | 0.010767 | 0.022880 | 0.001346 | 0.000000 | 0.000000 | 0.000000 |
| 5.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.001346 | 0.012113 | 0.006729 | 0.004038 | 0.014805 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 6.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.002692 | 0.002692 | 0.000000 | 0.005384 | 0.001346 | 0.000000 | 0.000000 | 0.000000 |
| 6.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.002692 | 0.002692 | 0.001346 | 0.000000 | 0.002692 | 0.000000 | 0.000000 | 0.000000 |
| 7.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 | 0.004038 | 0.000000 | 0.000000 | 0.000000 |
| 7.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 | 0.000000 | 0.000000 | 0.001346 | 0.008075 | 0.000000 | 0.000000 |
| 8.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.002692 | 0.002692 | 0.000000 |
| 8.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 | 0.001346 |
| 9.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 9.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 | 0.000000 |
| 10.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 |
| 10.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.001346 | 0.001346 |
The capture_length_matrix function can also be used as an arbitrary matrix generator. To do this, simply pass a different Series in the place of capture length (L). For example, while not specified by the IEC standards, if the user doesn’t have the omnidirectional wave flux, the average power matrix could hypothetically be generated in the following manner.
[10]:
# Demonstration of arbitrary matrix generator
PM_mean_not_standard = wave.performance.capture_length_matrix(
Hm0, Te, P, "mean", Hm0_bins, Te_bins
)
The capture_length_matrix function can also use a callable function as the statistic argument. For example, suppose that we wanted to generate a matrix with the variance of the capture length. We could achieve this by passing the NumPy variance function np.var into the capture_length_matrix function, as shown below.
[11]:
# Demonstration of passing a callable function to the matrix generator
LM_variance = wave.performance.capture_length_matrix(
Hm0, Te, L, np.var, Hm0_bins, Te_bins
)
Power Matrices
As specified in IEC/TS 62600-100, the power matrix is generated from the capture length matrix and wave energy flux matrix, as shown below
[12]:
# Create wave energy flux matrix using mean
JM = wave.performance.wave_energy_flux_matrix(Hm0, Te, J, "mean", Hm0_bins, Te_bins)
# Create power matrix using mean
PM_mean = wave.performance.power_matrix(LM_mean, JM)
# Create power matrix using standard deviation
PM_std = wave.performance.power_matrix(LM_std, JM)
# Show mean power matrix, round to 3 decimals
PM_mean.round(3)
[12]:
| y_centers | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 | 11.0 | 12.0 | 13.0 | 14.0 | 15.0 | 16.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x_centers | |||||||||||||||||
| 0.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 0.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 224.996 | 117.594 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 1.0 | NaN | NaN | NaN | NaN | NaN | NaN | 212.762 | 202.713 | 188.707 | 187.103 | NaN | 213.926 | 174.154 | 164.886 | NaN | NaN | NaN |
| 1.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 176.402 | 199.802 | NaN | NaN | 201.883 | 191.598 | 221.705 | 190.124 | NaN | NaN |
| 2.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 203.667 | 216.857 | 192.965 | 201.633 | 216.268 | 209.634 | 162.569 | 232.530 | NaN | NaN |
| 2.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 193.397 | 203.529 | 196.907 | 212.883 | 211.277 | 202.760 | 199.263 | 272.421 | NaN |
| 3.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 170.739 | 216.459 | 197.484 | 200.895 | 212.107 | 193.837 | 222.185 | 169.497 | 122.296 | NaN |
| 3.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 194.894 | 214.108 | 202.725 | 206.901 | 184.099 | 186.077 | 221.659 | 186.201 | NaN |
| 4.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 217.289 | 189.403 | 201.362 | 207.532 | 207.971 | 172.771 | 213.854 | NaN | NaN |
| 4.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 197.994 | 194.238 | 205.559 | 203.195 | 197.980 | NaN | NaN | NaN | NaN |
| 5.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 198.149 | 196.527 | 222.219 | 215.221 | 204.002 | 254.004 | NaN | NaN | NaN |
| 5.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 249.158 | 212.561 | 212.734 | 168.655 | 208.220 | NaN | NaN | NaN | NaN |
| 6.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 182.314 | 159.418 | NaN | 208.418 | 241.347 | NaN | NaN | NaN |
| 6.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 164.712 | 233.890 | 110.517 | NaN | 207.919 | NaN | NaN | NaN |
| 7.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 155.691 | 229.022 | NaN | NaN | NaN |
| 7.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 166.855 | NaN | NaN | 128.897 | 198.053 | NaN | NaN |
| 8.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 230.281 | 184.510 | NaN |
| 8.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 248.338 | 264.534 |
| 9.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 9.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 116.230 | NaN |
| 10.0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 244.634 |
| 10.5 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | 190.849 | 212.411 |
Calculate MAEP
There are two ways to calculate the mean annual energy production (MEAP). One is from capture length and wave energy flux matrices, the other is from time-series data, as shown below.
[13]:
# Calcaulte maep from timeseries
maep_timeseries = wave.performance.mean_annual_energy_production_timeseries(L, J)
print("MAEP from timeseries = ", maep_timeseries)
# Calcaulte maep from matrix
# See Issue #339
# maep_matrix = wave.performance.mean_annual_energy_production_matrix(
# LM_mean, JM, LM_freq
# )
T = 8766 # Average length of a year (h)
maep_matrix = T * np.nansum(LM_mean * JM * LM_freq)
print("MAEP from matrices = ", maep_matrix)
MAEP from timeseries = 1767087.527586333
MAEP from matrices = 1781210.8652839188
Graphics
The graphics function plot_matrix can be used to visualize results. It is important to note that the plotting function assumes the step size between bins to be linear.
[14]:
# Plot the capture length mean matrix
ax = wave.graphics.plot_matrix(LM_mean)
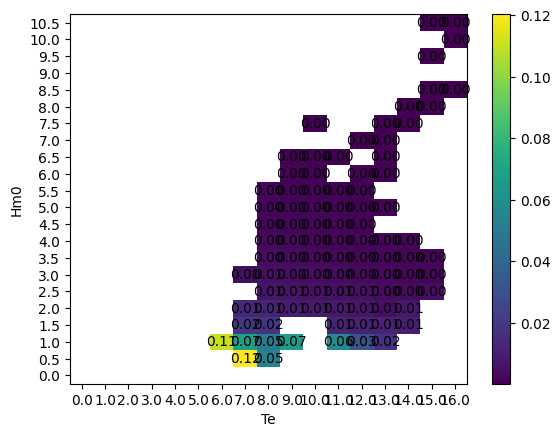
The plotting function only requires the matrix as input, but the function can also take several other arguments. The list of optional arguments is: xlabel, ylabel, zlabel, show_values, and ax. The following uses these optional arguments. The matplotlib package is imported to define an axis with a larger figure size.
[15]:
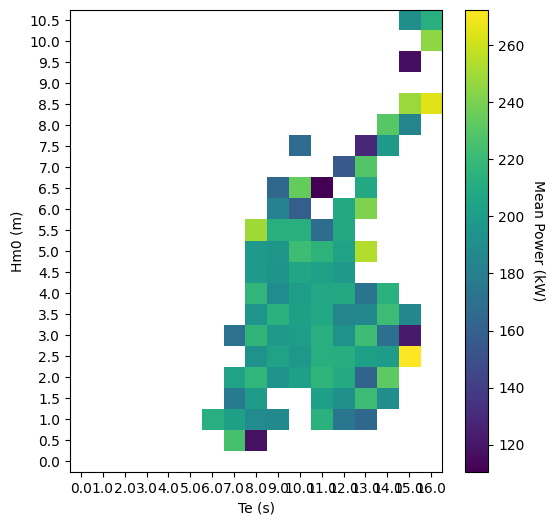
# Customize the matrix plot
import matplotlib.pylab as plt
plt.figure(figsize=(6, 6))
ax = plt.gca()
wave.graphics.plot_matrix(
PM_mean,
xlabel="Te (s)",
ylabel="Hm0 (m)",
zlabel="Mean Power (kW)",
show_values=False,
ax=ax,
)
[15]:
<Axes: xlabel='Te (s)', ylabel='Hm0 (m)'>
